Q4E Case Study 25
- Gravity ' Estimating the Magnitude'
|
Proposed subject useage |
|
|
Sports Science / Mathematics / Physics (A/AS level / Degree Yr 1/2) |
|
Introduction
Gravity acts on any object with mass, and causes said object to be accelerated towards the centre of the Earth at a constant rate, producing the force known as weight. Acting purely in a vertical direction, gravity accelerates objects downwards, and if this object is not in contact with the ground (i.e. is a projectile), then its vertical velocity increases in a downward direction. When in contact with the ground, a reaction force is exerted to equal the force produced due to the acceleration of gravity (using the principles of both Newton’s 2nd Law of acceleration (F=ma), and Newton’s 3rd Law of Action Reaction). However, when an object is a projectile, the only other force exerted is that of the resistive force of air resistance. For this particular case study, air resistance was ignored as its magnitude was considered to have negligible affects on the flight of the ball. Therefore the acceleration of the ball was considered a direct cause of the affects of gravity.
At ground level on the surface of the Earth, gravity is widely accepted to have a value of -9.81 m∙s-2. For this case study, this was the value to which comparisons were made. (It is important to note that this negative sign does not mean that the object is slowing down (decelerating), but indicates the direction in which gravity acts. When using the convention of positive travel being upwards, a negative acceleration just means that an object is accelerating in a negative direction, i.e. accelerating downwards)

Figure 1: Pictorial depicition of the forces considered acting on the ball
Scientists have been investigating the effects of gravity for hundreds of years. Initially Galileo used observations of pendulums, masses falling in vacuums and objects moving down inclined planes to conclude a uniform rate of acceleration, but this was not quantified. Today, scientists use sophisticated equipment such as lasers, to measure the velocity of falling masses, or a gravity meter whereby a mass is suspended on a spring, with the stretch of the spring being proportional to gravity.
Objectives of this study:
To demonstrate the effect of gravity and use calculations to predict its magnitude.
-
Test the effectiveness of different recording equipment (cameras) and different frame speeds to accurately capture the dropping of a ball.
-
Compare values taken from video footage to that of -9.81 m∙s-2, ultimately testing the effectiveness of the Quintic digitisation and linear analysis functions.
-
Use regression analysis to calculate acceleration due to gravity from the raw data exported from Quintic Biomechanics.
Methodology:
-
A golf ball was dropped from a consistent height (approximately 1.5 m) six times.
-
Video footage was captured using three different pieces of equipment set at different frame speeds;
- Casio Exilim FH20 HD - 30 fps (Pixel size: 1280 x 720)
- Quintic High Speed USB2 Camera - 41.12 fps (232 x 474)
- Panasonic Digital Video Camera (NV-GS230) - 50 fps (720 x 576)
- Quintic High Speed USB2 Camera -100 fps (400 x 480)
- Casio Exilim F1 - 300 fps (384 x 512)
These were set up approximately 3.5 m away from the dropping ball, and at staggered heights to allow simultaneous capture.
-
Videos were captured simultaneously so that between-equipment values were comparable.
-
Captured videos were opened in the Quintic Biomechanics v21 software, where the clips were calibrated, digitised (both at full zoom capacity, and at normal size), smoothed and analysed.
-
Data was exported to an excel file where averages and standard deviations (SD) were calculated and examined. The first six frames were ignored, as were the last six frames (due to Butterworth Filters taking time to adjust the data).
-
Multiple regression equations were carried out on the raw data.
-
Subjective judgment was employed to account for outliers.
-
Graphs were constructed from the exported data to further analyse the results.
Functions of the Quintic software used:
Butterworth Filters:
A Butterworth filter constructs a flat response in the determined passband, resulting in a smoother digitisation trace, and thus reducing error associated with the manual digitisation procedure. The filter values displayed in Table 1 are the optimums that have been applied to the data to smooth out any anomalies that may have occurred during the digitisation process. These ‘Optimal Butterworth Filter Values’ are calculated via the Quintic software for both X and Y.
There was little difference between the ‘Raw and Smoothed Data’ in the Y direction for the example shown below (Casio 300 fps, Zoomed). It can be seen in the top left box of Figure 2 that the smoothed green curve lies very close to the original trace of the raw data (red line). Moreover, the residuals (bottom left box in Figure 2), show the difference between the raw and the smoothed data, and as these values oscillate around 0.
Table 1: Butterworth filter values

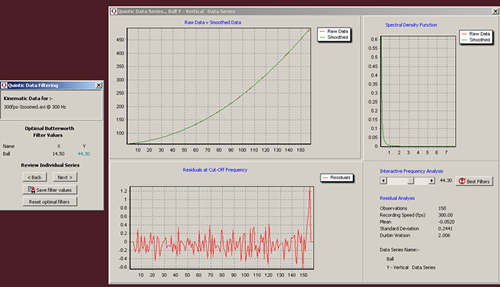
Figure 2: Quintic filtering screen (Casio F1 300 fps, Zoomed digitising)
Results:
The figures below show how the vertical position of the golf ball changes as each frame passes (each red line depicting a different frame). It can be seen that as time progresses, the distance travelled per frame increases, meaning that the object is travelling faster each frame (velocity = distance ÷ time, where for this example time is constant, and so an increased distance results in an increase in velocity), and thus is accelerating. As previously stated, this acceleration is a direct result of gravity.
It can be seen below (Figure 3-5) the real effect of using different frame speeds to capture videos. In each clip the ball is accelerating at the same speed, and is thus travelling the same distance in the same period of time. The concentration of the horizontal lines is dependant on how many occasions in this time period the equipment takes a picture (i.e. its frame speed). At a higher frame speed, more images are captured per second and so the lines are more concentrated as the ball has a shorter time over which to drop, thus dropping a shorter distance. When detail is required it is advised a high frame rate is utilised.

_Figure 3 ______________Figure 4__________________Figure 5
Both Table 2 and Table 3 show the vertical accelerations calculated (one for digitising utilising a full zoom (Table 2), and the other without). These values are based on an average of frame by frame calculations of acceleration at each stage of each ball drop. These were then averaged for each piece of recording equipment to give an overall value for each method. The standard deviations (SD) show the spread of the data from the mean, and can help to analyse the consistency of the equipment in predicting acceleration due to gravity. The larger the SD, the more varied the values calculated. It can been seen highlighted in Table 2 that Drop Number 1 for the Quintic High Speed USB2 camera (41.12 fps) seemed to be anomalous when compared to the other repeats. Similarly the same judgement was made in Table 3 for Drop Number 5 of the Casio (300 fps). Therefore, the columns on the far right exclude these values, to give values which were not skewed by suggested outliers.
Table 2: Average vertical accelerations for zoomed digitising

Table 3: Average vertical accelerations for non zoomed digitising


Figure 6: Quintic Biomechanics v21 screenshot of Multi-Linear Analysis
Figure 6 above shows all six of the drops for the zoomed Casio 300 fps camera, with the black lines depicting each repeat, and the red depicting the average of all drops.
Figure 7 and 8 display the individual accelerations calculated for each repeat using all equipment, and makes comparisons to the accepted value of gravity (displayed on the graphs as the horizontal red line). These visual depictions make it easier to both identify anomalous values, and also see which equipment gave more precise and accurate values. Drawing information from both graphs, it can be seen that the apparatus giving the best predictions was that of the Quintic High Speed USB2 Camera for both frame speeds as the calculated values lay closest to and most consistently with the line set to depict gravity.

Figure 7: Average vertical accelerations for zoomed digitising

Figure 8: Average vertical accelerations for non zoomed digitising
The results also suggest that there is no substantial difference to be found between the methods of digitisation and the level of zoom utilised, with no one technique performing consistently better. Small random variations between methods may be due to human error in manually digitising. To investigate this, 6 drops from one piece of equipment (High Speed (100fps)) were manually digitised on two separate occasions, and then the values calculated compared. This is summarised below in Table 4.
Table 4: Investigating human error during manual digitisation

It can be seen that there are very small, random percentage differences between the digitisation attempts (1 and 2), with the maximum variation being 2.13%, accounting for a difference in acceleration of roughly 0.2 m∙s-2, with the least variation being 0.31% (approximately 0.03 m∙s-2). This shows that human error does occur during the manual digitisation process, and this would affect the predictions of gravity calculated.
Another aspect which warrants consideration is the fact that the software can only work to a level of accuracy determined by the clip. Take for example the videos from the Casio (300 fps) camera. These had a vertical image size of 511 pixels, with each pixel representing a certain distance (determined by the calibration procedure). Digitisation can only occur to a maximum of to the nearest third of a pixel (only when using zoomed digitisation, being less if the zoom is not utilised), and so distances can only be calculated to within these limits. This may slightly alter the accelerations calculated, as distances may not be accurate. Taking this into consideration, it may be suggested that even though substantial differences were not found, digitising the clips using a higher level of zoom may be advantageous. This may also be the case when calibrating. The software can only be as accurate as the information provided, so if the calibration file is not an accurate representation of the distances, gravity values cannot be expected to be accurate. Again this is due to human error and the pixel size.
Intermediate Conclusion:
To conclude, the choice of recording equipment does make a difference to calculations. This is because the software and the results it can produce are reliant on the quality of the clip provided. From this experiment it appears that the best estimation of gravity can be obtained by utilising the Quintic High Speed USB2 Camera set at 100 fps, which consistently gave relatively precise estimations. The fact that the software was able to predict a value for gravity acceptably close to the acknowledged true value of acceleration (-9.81 m∙s-2) despite variations due to human error demonstrates the validity of Quintic Biomechanics v21.
Calculating gravity using multiple regression:
The data was then analysed using the multiple regression function in Excel to see what values the raw data exported from Quintic Biomechanics v21 gave for gravity. This was used as an alternative method to using the Quintic software to calculate gravity (but still utilized Quintic’s raw data). All of regression values calculated were significant to at least p≤0.05. The values obtained for gravity can be seen below in Table 5 and Table 6.
Table 5: Average vertical accelerations from zoomed digitising

Table 6: Average vertical accelerations from zoomed digitising

As for the previous tables in the case study, the highlighted values indicate where subjective judgement identified anomalous values.
The figures below (9 and 10) help to visually confirm the outliers as well as making comparison to the accepted value of gravity for each (depicted by the red line).

Figure 9: Average vertical accelerations for zoomed digitising
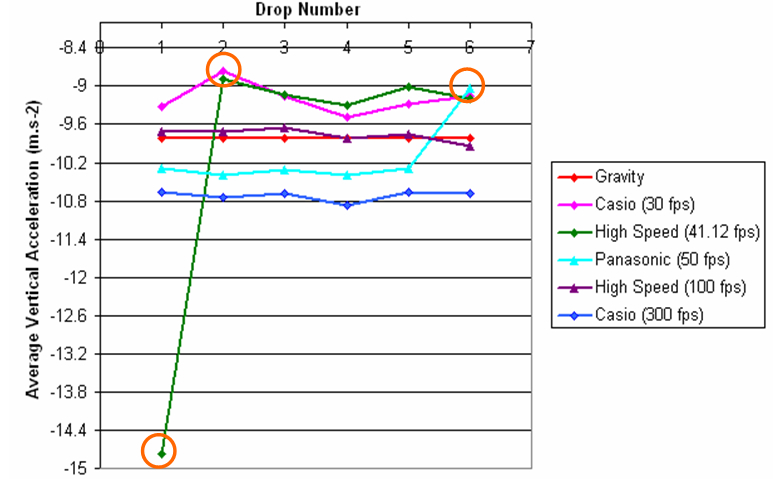
Figure 10: Average vertical accelerations for non zoomed digitising
Intermediate Conclusion:
Drawing on information from both tables and figures, the method using the zoomed digitisation function produced more accurate results when compared to the non zoomed data, as can be seen from Figure 9 where the majority of the lines (excluding the Casio 300 fps) lie closer to the line depicting gravity. In terms of the choice of the equipment, when considered across both digitisation methods, as before the Quintic High Speed USB2 Camera (when set to 100 fps) appears to give the most accurate results from the averages obtained. The results were similar to those calculated through averaging.
Conclusion:
Across both parts of the case study there was one piece of recording equipment which did not produce the results expected, and this was the Casio Exilim F1 when set to a frame speed of 300 fps. At higher frame speeds one would expect that the data would produce more accurate results, as more frames means that more information is gathered on the flight path of the ball, and less information is lost. However, although consistent (small standard deviations) for both the results of the Quintic and the regression analysis, the predicted gravity values were not as accurate as expected, often over predicting the acceleration.
A reason for this inaccuracy between accepted acceleration and those calculated could have been a result of the calibration procedure (although this would have affected all pieces of equipment). If the distances measured were not precise then all values calculated will not be a true representation. Another point to consider is where the calibration measurements took place. For this investigation, measurements were taken of a door in front of which the golf ball was dropped. This in itself may cause inaccuracy as the measurements taken were not on the same plane to the flight of the ball. As depicted in Figure 11 and 12, the calibrated length is greater than the distance over which the ball falls. Therefore, the Quintic software will overestimate the distance the ball falls if dropped in front of the plane of calibration.

Figure 11: Affect of calibration plane in relation to the plane of action
The numerical effect of this can be seen in an example below.

Figure 12: Similar triangles
|
By considering the ratio of the lengths of the sides of the similar triangles (highlighted in green and purple):
Horizontally:
3.3 ÷3.5 = 0.943 (3.s.f)
Therefore, vertically (y and x):
x ÷ y = 0.943
x = 0.943y
|
This shows that the x value (i.e. the distance the ball has dropped) is smaller than the y value (the calibration distance) by a factor of 0.943. This confirms that the values from the software will be overestimating the acceleration due to gravity as the ball has not dropped as far as the computer is suggesting. Additionally, as there was no marker indicating a horizontal distance away from the plane of the ball, the size of which a correction factor would need to alter would vary between drops, and this may be another reason as to why the values calculated in this case study were not consistently different, but fluctuated around the accepted value. To show the effect that this could have had on the results collected, the correction factor of 0.943 was applied, and the corrected values can be seen below in Table 7.
Table 7: Corrected average vertical acceleration values

In general it can be seen that by using higher frame speeds and utilising the zoom function when digitising gives predictions closer to the acknowledged value. To conclude, there are many different considerations that must be taken into account in order to produce accurate and precise estimation of gravity, from the equipment and set up you use to the accuracy of digitisation. It is important that as many of these variables as possible are considered, and that the detrimental effects they could have on calculations minimised if accurate predictions are to be made. However, when compared to the cost and expertise required for the methods and equipment utilised by scientists, the estimations collected in this case study are a practical method of estimating gravity.

Downloads:



