Q4E Case Study 19 - Simple Harmonic Motion
Proposed Subject usage:
Mathematics / Physics (A/AS level),
Sports Science (Degree Yr 1/2)
Introduction
In classical mechanics a harmonic oscillator is a system, which when displaced from its equilibrium position, experiences a restoring force proportional to its displacement. This is described by Hooke’s Law and represented by the equation below;
 : equation 1 Hooke’s Law : equation 1 Hooke’s Law
Where;
F is the restoring force
x represents the displacement from the equilibrium
k is a positive constant
If F is the only force acting on a system, the system is called a simple harmonic oscillator and it is said to undergo simple harmonic motion (SHM). SHM is a motion that is neither driven nor damped (i.e. no friction to slow the pendulum down); the motion is periodic as it repeats itself at standard intervals in a specific manner. It can also be described as the repetitive back-and-forth movement through a central or equilibrium position in which the maximum displacement on one side is equal to the maximum displacement on the other. SHM is characterized by its amplitude (maximum distance that the mass is displaced from its equilibrium), its period (time for a single oscillation), its frequency (the number of cycles per unit time) and its phase (determines the starting point on the sine wave). The period and frequency are constants determined by the overall system, while the amplitude and phase are determined by the initial conditions of that system.
 A pendulum consists of a weight or bob being suspended from a pivot where it can swing freely, furthermore a simple pendulum is one where the mass is the same distance from the support point, like a ball on the end of a string. This type of pendulum is an example of motion that is approximately a Simple Harmonic Oscillator (SHO). A simple pendulum demonstrates simple harmonic motion under the conditions of no damping and small amplitude. The motion of a simple pendulum can be considered SHM even though the bob hanging at the end of the string moves in a curve because if the string is relatively long compared to the initial displacement, the curve made by the bob is almost a straight line. In a pendulum the force is always acting in the opposite direction to that of the displacement and the bob is moving the fastest when it passes the lowest point (point 2 on illustration below).
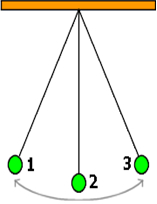
Objectives
- Calculate the period of the pendulum as well as testing the new Quintic digitisation function.
- Using Quintic software investigate if Hooke's Law holds true for the pendulum i.e. that the restoring force applied to the pendulum is proportional to the displacement.
- Examine the relationship between the systems velocity and displacement.
Methods
The videos have been digitised and calibrated using the Quintic Biomechanics v17 software.
- A simple pendulum was created by hanging a mass less string of length 1.23metres from a pivot with a bob attached of weight
2.2 grams.
- Video footage was captured of the oscillating pendulum at 300 fps using a Casio exilim F1.
- The captured video was opened in the Quintic Biomechanics 9.03 v17 where the clip was calibrated, digitised and analysed.
- Data was exported to an excel file where the variables were calculated and examined.
- Graphs were prepared from the exported data to further analyse the pendulum system.
Functions of the Quintic software used:
- Single Camera System
- One-Point Digitisation Module
- Butterworth filter
- Calibration
- Interactive Graph and Data Displays
- Export Data
- Shape Tools
- Markers Function
Results
Formula for Period of a Pendulum

where;
t = period
l = length
g = gravity
It is well accepted that acceleration due to gravity on earth is represented by the value 9.81 ms-2. By rearranging the formula above to solve for gravity we can solve for this known value and hence test the new Quintic digitisation module. The period was calculated using the Quintic software by timing 12 oscillations using the marker function and then the average time of these oscillations was calculated (t=2.29) in order to determine an accurate value for the period of the pendulum. The rearranged formula is represented below with the unknown value being gravity.
If the suspended bob is displaced to the left or right, it will swing freely back and forth under the influence of gravity. For small horizontal displacements such as the oscillations of the simple pendulum, the restoring force on the suspended bob can be given by:

In the equation above m represents the mass of the bob, g the magnitude of the gravitational acceleration, L the length of the string of the pendulum and x is the horizontal displacement. The presence of the minus in the formula shows that the restoring force acts in a direction opposite to the displacement. Since m, g, and L are positive constants, we note that equation 2 has the same form as equation 1 for Hooke’s Law. Recall that Hooke’s law is of the form (F = -k x).

Graph 1
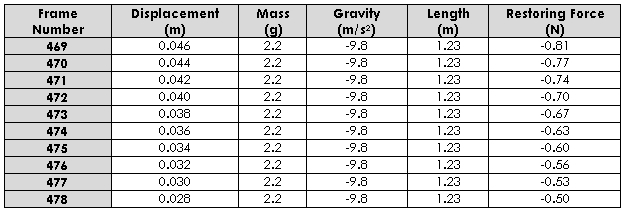
Table 1
Graph 1 represents the restoring force experienced by the pendulum plotted against the displacement relative to its equilibrium position. The calculations are based on 10 consecutive frames during an oscillation as shown in the data table 1 above. The restoring force is a variable force that gives rise to equilibrium in a physical system i.e. the force is always trying to restore the pendulum to its equilibrium position. Both graph 1 and table 1 illustrate this because as the system gets closer to its equilibrium there is a marked decrease in the restoring force. This also demonstrates the relationship between the displacement and restoring force. At maximum displacement the highest restoring force occurs, a decrease in the displacement results in a corresponding decrease in the restoring force. Similarly at minimum displacement the lowest recording of the restoring force occurs. This shows that the variables are directly proportional to one another and is further demonstrated by the straight vertical line occurring in the graph. This relationship also provides evidence to support Hooke’s Law which states that when an oscillator is displaced from its equilibrium position it will experience a restoring force proportional to the displacement.
Graph 2 : Velocity and displacement plotted against time.
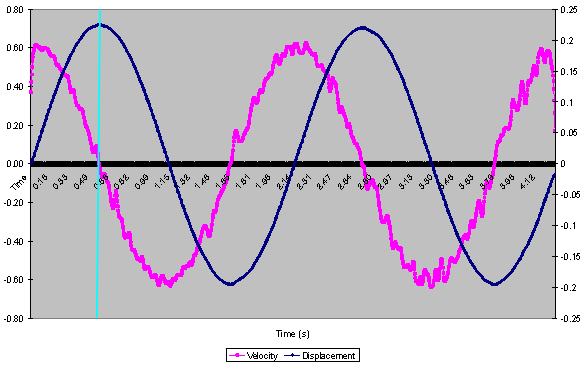
Graph 2 represents velocity and displacement plotted against time. It is evident that an indirect relationship exists between the velocity and displacement values recorded. As the displacement reaches maximum the corresponding velocity value as a function of time is at its minimum value, this is denoted in the graph by the blue line. Also the graph shows that velocity is at its maximum value as the bob reaches its lowest point (equilibrium position) and at a minimum value when the system reaches maximum displacement. The graph also illustrates that the movement of the pendulum is periodic as it repeats itself at specific and standard intervals.
Conclusion
The experimental value of gravity calculated by the Quintic software was numerically equal to the value accepted as the earth’s gravitational acceleration demonstrating the validity of the Quintic Biomechanics 9.03 v17 software. In the small angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. A simple harmonic oscillator experiences repetitive back-and-forth movement through a central, or equilibrium position. When a simple pendulum is displaced from its equilibrium position it experiences a restoring force proportional to its displacement showing that a direct relationship exists between the variables while also proving the pendulum exhibits Hooke’s Law. Finally when velocity is at a maximum the corresponding displacement value will be at its minimum value demonstrating an indirect relationship between these variables.
Downloads
Written
Case Study |
Video avi.
file |
|

~0.25 MB |

~6.80 MB |

~0.65 MB |
|



